The Challenge of Change . . .

I recently had an "ah ha" moment in a meeting as we were debriefing a powerful TED Talk by Diana Laufenberg. There is no doubt that teaching is one of the most challenging professions.  Even over the last 15 years, teaching has become much more demanding of our classroom teachers.  It makes me wonder if we as educators are putting more stress on ourselves because it's easier to do things the way we have always done them verses embracing change!

Our society has changed drastically over the years due to technology and the way that we can readily access information. But . . .  when you think about it, "school" really has not changed much from when our own parents attended.   

Take a minute to watch this TED Talk and think about how can we allow students to fail and empower their voice.



We are fortunate that Diana Laufenberg will be part of this year's Leander ISD Continuous Improvement Conference.  I look forward to learning more from her and seeing you all at our 20th annual conference!  

Counting Collections and Giveaway!

Although counting is one of the best ways to help children develop number sense and other important mathematical ideas, we do not do enough of it in elementary schools.

Why should I do counting collections?
Children need many and varied experiences with counting to learn which numbers come next, how this number sequence is related to the objects in front of them, how to keep track of which ones have been counted and which still need to be counted (Fuson 1988).

How do I begin?
It is as easy as placing a large pile of items on the tables and without any further instruction ask the students to begin counting their items!

Once you decide to make counting collections a regular routine in your classroom you will need to start collecting baggies of "stuff." Beans, pom-poms, buttons, cotton balls, rocks.... the sky is the limit!  A walk through a craft store will spark lots of ideas. Parents can donate collections are well. Make sure you have collections of different sizes to meet the students' different needs. You will need a method for the students to record their thinking. Math journals work great!

What does the teacher do as the students are working?
As students work in partners, the teacher is observing, taking anecdotal notes, asking reflective questions, and selecting students to share with the whole group.

Why do the students record their counts?
Most students will begin counting one by one with no strategy for grouping the items. Once the some time has passed, interrupt their counting and ask them a question and then tell them to continue counting. Many students will forget where they were and have to start all over! This is a perfect time to discuss strategies for grouping items and how they will record their counting in their journals.

What does Counting Collections look like in Kindergarten?


Counting Collections: Kindergarten - a common core classroom friendly exercise from Luna Productions on Vimeo.

What does Counting Collections look like in the older grades?


Counting Collections: Third Grade - a common core classroom friendly exercise from Luna Productions on Vimeo.

Are Counting Collections part of your math instruction?
Try backwards Counting Collections; You give the number and they make the collection!

Counting is fundamental to so many things we do in mathematics.  
Build their COUNTING POWER!!

To learn more read this article:
Counting Collections by Julie Kern Schwerdtfeger and Angela Chan in Teaching Children Mathematics / March 2007

For Leander ISD employees: To be eligible to win this amazing Counting Collections Starter Kit, add a comment below on how you would use this in your classroom. We will put all entries into the randomizer on Tuesday, January 29, 2013 @ 4 p.m.

We have a winner!  Heather Moseley from Bagdad Elementary - Congratulations. We hope you enjoy this amazing Counting Collections Starter Kit.  The contest is now over, but we hope everyone keeps on "counting!" 

Birds On A "Number" Line

What do you see?  

Call me crazy or math nerdy but I see a number line!

The traditional number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point.

In contrast to a traditional number line, an "open" number line is just an empty line that can be used to record children's addition and subtraction strategies. Only the numbers children use are recorded and the addition or subtraction is recorded as leaps or jumps.

Here are some examples of open number lines:

This example shows a student using incremental strategies. This means adding up in "chunks" or increments. One benefit is the students decide the "chunks" depending on the number choices.

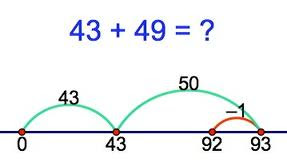This example shows a student using compensation. This means they add or subtract to adjust a number to make it friendly, solve the problem, and then readjust to find the solution.

This example shows a student a counting up for a subtraction problem. Look at the place value the student uses to compose and decompose the numbers.

Aren't open number lines awesome?  What a great way to model thinking!

So how do the birds on a line remind me of a number line? The birds just alway seem to be evenly spaced on the line so it just got me thinking about number lines!

Here is a problem to ask your students:

Name points A, B, C and D on the number line.  Justify your solution.

The next time you see birds just hanging out on the lines, I dare you not to think of a number line!

Can you think of any other real-life objects that remind you of number lines?